Feedback

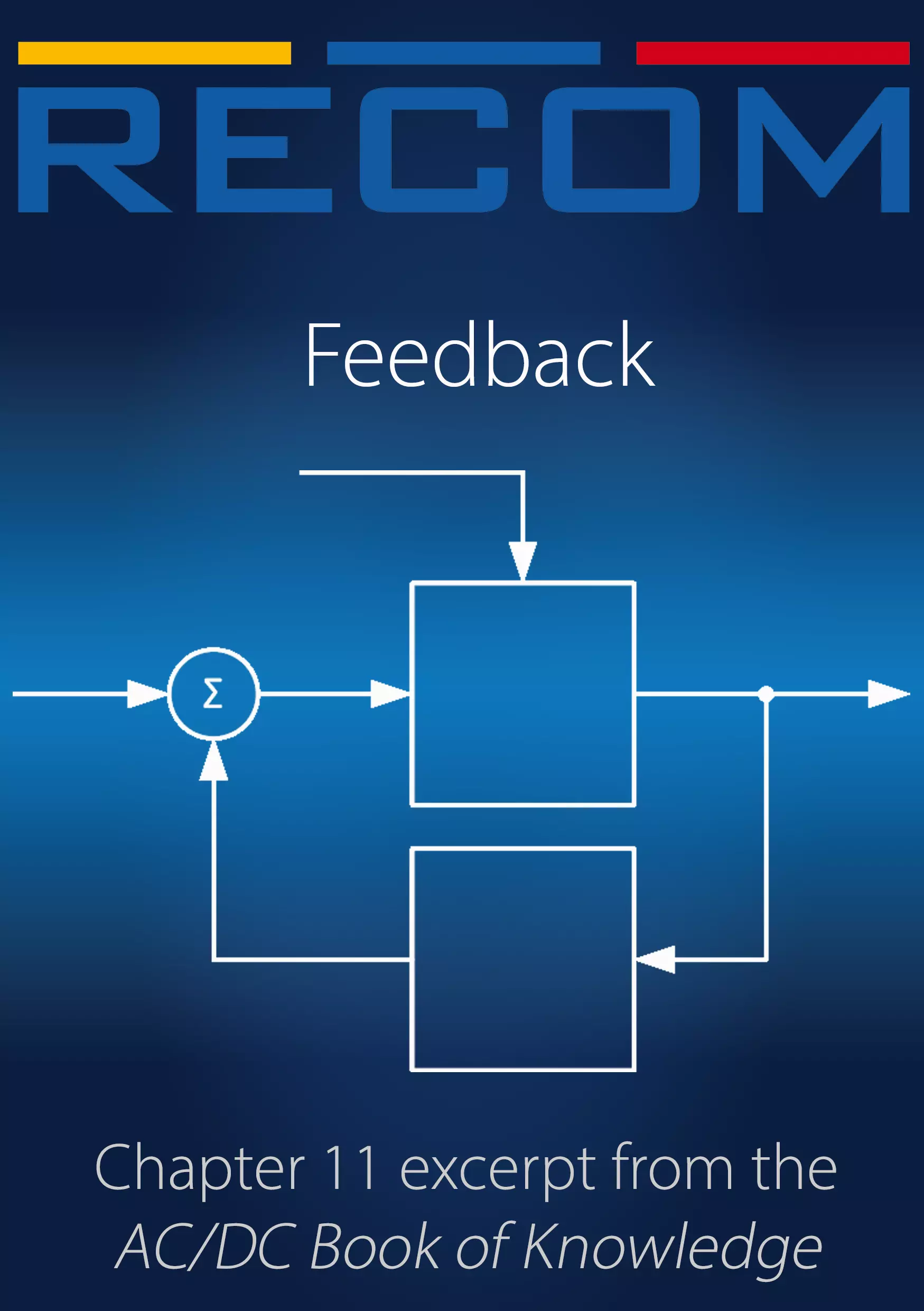
The general arrangement for any closed loop system is shown below:



There are two gain blocks: G which represents the power gain and H which represents the feedback gain (which is normally less than one, i.e. attenuation). The summing point has a non-inverting reference voltage input and an inverting input for the feedback signal (Negative feedback). The (S) suffix indicates that these two gain blocks are in the S-domain, i.e., they have both DC and AC components. The AC component means that both the gains will change with frequency and that the differences in the frequency dependency will cause a phase shift in the feedback.

In the case of a power supply, the system input in the supply voltage and the system output is the output voltage, but the feedback can be either current or voltage based.



Where the open loop gain, GOL(S) is:



The simplest implementation of such a closed loop power supply system is a type 1 feedback using operational amplifiers (Op-Amps).

Measuring Loop Stability

The degree of immunity to instability can be found by carrying out a bode plot test where small perturbations are injected into the feedback system and the response measured. This can be done using specialist equipment or tested by using standard laboratory equipment and an audio transformer:



Practical Tip: In practice, the choice of audio transformer, shunt resistor and way the test leads are connected influence the measurements considerably. You will get more accurate results using a commercially available frequency analyser with matched injection isolation transformers than if you attempt to make your own.

The phase margin is the number of degrees of phase when the gain is zero. The gain margin is the number of decibels of gain when the phase is zero. The combination of the two determines the loop stability.

The compensation is sufficient if the phase margin is 45° or higher and the gain margin is at least -6dB (preferably closer to -10dB). The margins need to be checked under all operating condition extremes (max Vin, min Vin, min. load*, max. load, min. temperature, max. temperature) to guarantee stable operation.

*NOTE: loop stability measurements can only be done on a constantly running system. If the AC/DC controller goes into pulse-skipping mode at low loads, then no proper measurements can be made.

The injection point in the loop is optimum if the impedance on one side of the injection point is much higher than on the other, for example between the low impedance output stage and the high impedance resistor divider to the feedback comparator (as shown below in Figure 5). It would also be possible in theory to inject the signal between the comparator output and PWM controller input, but in many controller ICs, this point is internal inside the IC and not accessible.



However, for high voltage outputs such as a PFC stage, the injection point shown in figure 5 is not ideal. This is because the perturbation signal is so attenuated by the high resistance voltage divider that the measurements become unreliable. In this situation, an additional buffer op-amp can be used to allow the signal to be successfully injected. The op-amp is unity gain, so will not affect the readings as long as it has a high enough bandwidth.



If the injected perturbation signal is too weak, then the measurements will become increasingly inaccurate at low frequencies because the signal-to-noise ratio will be too low. If the injected signal is too strong, then the measurements will become erratic at higher frequencies as the perturbations will over-ride the internal feedback voltage levels.











Another way of visualizing the same gain and phase information is to use a Nyquist diagram. Most professional-grade frequency analysers can output the measurements as either a bode plot or a Nyquist diagram. The advantage of a Nyquist diagram is that not only the gain and phase margins can be determined, but also the stability margin, which occurs at the frequency where the curve is closest to the (-1,0) point (refer to Fig. 9).
The factor -1 takes into account the -180° phase change implicit in negative feedback. The Nyquist diagram can also be reflected along the imaginary axis to show the instability point at (1,0) for the entire feedback loop.



The phase reserve is the angle between the plot and the real axis where it crosses the -1,0 circle. The amplitude reserve is the separation between the plot and the -1,0 point measured along the real axis.

The stability reserve is the separation between the plot and the -1,0 point measured at its closest approach.

Type 1 Feedback Loop Compensation Calculation

It is also possible to determine stability by calculation, depending on the type of compensation circuit used in the feedback loop.
A Type 1 feedback is shown below in both voltage (output voltage controlled by input voltage) and transconductance (output current controlled by input voltage) variants:



For example, if the desired output voltage is 5.0 volts and the reference voltage is 2.5 volts, then resistor R1 will be made equal to R2 so that the output voltage is divided by two.

These circuits are integrators: sudden changes in the input signal are turned into a more slowly ramping output signal which gives the power supply some immunity from breaking into oscillation by over correcting for changes in load or input voltage. The output ramp rate is dependent on R1 and C1 only, R2 plays no role in integration coefficient.
The gain/phase response for a type 1 feedback system is shown below:



The point at which the gain = 1 is the system zero.

For voltage Feedback:



For transconductance feedback, the transfer function is: (written in the s-format)



Practical Tip: The choice of the resistor values used in the divider network is unimportant for the transconductance circuit as only the ratio affects the gain. The circuit would have the same frequency response if either two 10k resistors or two 100k resistors were used for R1 and R2, for example. However, in the voltage feedback version, R1 appears in the frequency equation but R2 does not. Changing R1 from 10k to 100k would alter the gain plot. Therefore, if the output voltage needs to be trimmed when using voltage feedback, only R2 should be made variable and R1 kept fixed.

The slope of the gain is -20dB per decade, defined by the classic integration function of R1 and C1. If the op-amp has an ideal linear response time to small signal changes, then both the gain slope and the phase shift are constant over frequency. This can become a problem with repetitive or sudden step changes in the load or supply voltage. At higher frequencies than the system zero, the power supply struggles to maintain regulation as the phase and gain margins are too low.

Type 2 Feedback Loop Compensation

A solution to the problem of low gain and phase margins is to selectively boost them at higher frequencies. The Type 2 feedback circuit and gain and phase frequency responses are shown below:



As is evident from the frequency graphs in Fig 13, the additional C2 and R3 components have added both a gain boost and a phase boost at higher frequencies. The phase boost is limited to 90°, meaning that the maximum overall phase shift is 180°C. The peak of the phase boost response lies at the half way point between the zero and pole frequencies.



The new relationships are (assuming that C2 is much larger than C1):

Type 2 voltage feedback:



Type 2 transconductance feedback transfer function (written in s-format)



This equation combines the three main factors of the DC gain and the zero and the pole terms, which individually can be derived from the following relationships:





The gain at the crossover frequency is:



Type 3 Feedback Loop Compensation

In some fast transient response power supply circuits, even the additional gain and phase boost created by the Type 2 compensation may not be sufficient. This is especially true for CCM power stages that suffer from a large phase swing when the resonant frequency is exceeded.

Type 3 compensators place an additional “speed up” circuit across the input voltage potential divider:





As is evident from the frequency graphs, the additional C4 and R4 components have added more gain and a phase boost at higher frequencies. The phase boost is now more than 90°, meaning that the maximum overall phase shift is 225°C. The new relationships for Type 3 voltage feedback are (assuming that C2 is much larger than C1 and R1 is much larger than R4):



Type 3 transconductance feedback transfer function (written in s-format)



This equation combines the five main factors of the DC gain and the four zero and the pole terms, which individually can be derived from the following relationships:





The gain at the crossover frequency is then:



Optocoupler Feedback Loop Compensation

In practice, most AC/DC power supplies require input/output isolation. The feedback path is no longer direct but via an opto-isolator which also has a frequency dependent response. The most common opto-coupler circuit uses the 431 shunt regulator to control the optocoupler LED current. The 431 is a very versatile IC that acts like a tuneable Zener diode. A typical circuit is shown below:



In this circuit, R1x and R2x define the shunt regulator (IC1) threshold voltage (and therefore the output voltage regulation point), R_LED is the current limiting resistor for the optocoupler LED and Cx is used to define the AC response of the 431 IC. On the primary side, the phototransistor bypasses R1, filtered by the R_opto, C_opto components.

If the output voltage rises too high, IC1 starts to conduct more current and the LED shines more brightly, causing the phototransistor to bypasses more current and pull the junction of R1 and R2 closer to Vcc, regulating the output voltage down. If the output voltage falls, the optocoupler LED current is decreased and the R1 bypass current also decrease causing the junction voltage of R1 and R2 to drop, forcing the op-amp to increase its output drive to compensate. The feedback is thus a closed loop, even though the output is galvanically isolated from the input.



The over-and-under type (fig. 17a) typically has a transparent high dielectric strength film between emitter and receiver to improve the isolation withstand voltage. The total internal reflection type (fig. 17b) is a more complicated construction method, but does not need a separating film and has a lower coupling capacitance as the input and output planes are sideways on.

Adding these extra active components obviously affects the gain and phase frequency response of the feedback loop. If we take the simplest Type 1 comparator, the opto-coupler adds an additional pole and changes the flat phase response plot so that it behaves more like a type 2 feedback loop:



Practical Tip: The gain of the optocoupler (the current transfer ration, CTR) is both age and temperature dependent, which makes calculating the tolerances tricky. The datasheet CTR figure is usually given at 25°C, but it will increase if the temperature drops to the freezing point and decrease if the temperature rises. At 100°C ambient, the CTR will be around 70% of the datasheet value.

The main problem is that the optocoupler is typically positioned very close to the power transformer as they are both placed across the isolation gap. The transformer can run very hot under full load conditions and the heat radiating out can easily cause the CTR to become too low for proper regulation. The optocoupler output current can be increased by increasing the LED current, but then the no-load power consumption can become significant. Also the aging of the optocoupler is very dependent on the LED drive current, so increasing the LED current from, say, 5mA to 15mA will reduce the effective lifetime (the point where the CTR drops to 50% of its nominal value) from around 400k hours to 150k hours. Thus the position of the optocoupler on the PCB and its ambient temperature affects the optimal resistor values that need to be chosen!

Secondary side feedback compensation

It is also possible to add additional components to compensate on the secondary side for deficiencies in gain or boost. One common amendment is to add R_comp and C_comp components to cancel out the unwanted pole caused by the output capacitor’s own ESR:



Another useful secondary side compensation technique is to add HF bypass components across the LED current limiting resistor to increase the useful bandwidth of the opto-coupler (the response time is dependent on the LED current)



The gain/phase characteristic of a power supply will have multiple overlying components caused by the contributions from the power stage, compensation network and control loop elements. It is possible to calculate all of the terms involved and guarantee stability under all operating conditions by design, but confirmation by real-life measurement is needed to check that component tolerances and temperature effects do not cause the power supply to drift into a region where instability can occur.

Magnetic feedback

As mentioned previously, the CTR of an optocoupler varies with temperature and degrades with age. It also deteriorates when subjected to radiation in the form of neutron bombardment or gammas rays. The radiation permanently damages the sensitive photo junction in the receiving transistor as well as reducing the efficacy of the LED, eventually reducing the CTR to near zero. This makes optocoupler feedback undesirable for defense, space or high altitude applications.
An alternative to opto-coupled isolators is to use magnetic feedback. A separate transformer can be used to close the feedback loop while keeping the isolation intact. There are several ways of doing this:

Output side powered PWM feedback transformer.

A secondary side powered PWM oscillator drives a small signal transformer with a PWM signal that is proportional to the output voltage. The output winding on the primary side is rectified and smoothed to deliver a control voltage for the main switching oscillator:



Care needs to be taken to ensure that the circuit starts up correctly as the feedback regulation transformer is powered by the output voltage. Therefore the same circuit is shown here as used with the previous opto-coupler feedback design, R1 and R2 set the maximum permissible output voltage which can then only be regulated down by the feedback from the PWM oscillator. The PWM oscillator needs to run at a high enough frequency to ensure a fast response to load changes and to keep the ripple acceptable without making C_mag too big.

A good starting point would be x10 to x20 the main oscillator frequency.
The advantage of this design is that it will work with any single-output topology; forward, flyback or resonant. The disadvantage is that the response time is relatively slow, so it is not suitable for dynamic loads and that the output voltage always peaks to the maximum on power-up unless a soft-start circuit is used.

Direct magnetic feedback.

Forward converters rely on an output inductor to store energy and maintain the output voltage during the power transformer reset. The current in the output inductor ramps up and down continuously, so the inductor can be used as the primary winding of a feedback transformer without any additional circuitry on the secondary side. This solves one of the major problems of all secondary feedback circuits: namely how to reliably power the necessary feedback components on the secondary side? If the power supply is started up with a short or an overload on the output, then output regulation can be very difficult to control as the output voltage cannot stabilize.

With direct magnetic feedback, the voltage induced on the primary side winding of the feedback transformer is sampled just after the main power switch is turned off by a sample-andhold circuit and then buffered to be used to control the main oscillator:



The advantage of this circuit is the simplicity of implementation on the secondary side and its accuracy, as the sample-and-hold window can be adjusted to ignore any switching transients and to sample the induced output voltage only when it is stable. It also works well with multiple outputs that share a common output magnetic core (Fig 23). The induced feedback signal is then the summation of the output voltages.

The disadvantage of direct sampling is the difficulty of maintaining proper regulation under no load conditions. With no output load, the power switch on-time becomes very short and the sampling window even shorter. It can be nearly impossible to get an accurate feedback voltage to ensure proper regulation. Therefore, direct magnetic feedback should only be used with power supplies with a minimum load specification.



Primary side driven magnetic feedback.

One further method of implementing magnetic feedback deserves a mention, and that is a primary side driven signal transformer. This technique combines the previous two examples: a PWM-driven 1:1 transformer with fixed operating frequency and a simple sample-and-hold circuit to detect the appropriate measurement point in the cycle. Its main advantage that the secondary side feedback circuit is separately powered from the main power stage so will function correctly even if the output is turned off. The schematic is shown below in Figure 24:



The topology is essentially flyback. When the PWM signal is high, current flows through the primary winding and the transformer core becomes magnetized. Due to the reversed output winding, no current flows through the shunt regulator as the negative output voltage is blocked by the diode D1. When the PWM signal is low, the output voltage becomes positive as the magnetic field inside the core collapses, but is now clamped by the shunt regulator at a voltage determined by the output voltage V_out.

The reflected voltage on the primary side is the same as on the secondary side minus the diode drop, but with reversed polarity. The negative primary voltage can be sampled using the simple peak detector formed from D_S/H and C_S/H and then inverted or used as a negative reference voltage to modulate the feedback of the main power stage.



A practical circuit is shown below in figure 26 using a constant on-time PWM modulation signal.



A 1:1:1 transformer is used so that one output winding can be half wave rectified by D2 to create an isolated supply voltage for the shunt regulator. As this winding is not reversed with respect to the primary, the current that flows into C_cv is not measured by the hold capacitor C_H due to the blocking diode D_H (the voltage on the primary side is positive and equal to the voltage on the output capacitor C_CV minus one diode drop).

The voltage across C_H slowly charges up through R1B and R1B, “resetting- “ the negative hold capacitor voltage. When Q1 is switched off, the output voltages are reversed. Now D2 is reverse biased and D1 is forward biased.

The reflected primary winding voltage is negative and equal to the shunt regulator voltage plus the forward drop of D1. The voltage across C_H is pulled down via D_H to this negative voltage. If all of the diodes are the same with the same forward voltage drops, then the voltage across C_H is exactly equal to the shunt regulator voltage. Thus, the voltage on the hold capacitor is renewed every cycle and tracks changes in the output voltage accurately. Once the core has become completely demagnetized, then all of the diodes become reverse biased and no more current flows. At this point, the PWM signal should be triggered to start the next cycle so that the hold capacitor voltage does not droop.

The disadvantage of this technique is that the peak detector output is negative, so in some designs, it would need to be inverted with another op-amp stage to be useful. Secondly, the transformer must not go be allowed to go into saturation, so the core cannot be made too small even though the transmitted power is low. Finally, the value for C_H is a compromise between being high enough for low ripple and low enough for a fast response.

The advantages are the cycle-by-cycle tracking of the output voltage and the ability to operate at high ambient temperatures of 100°C or more as no opto-couplers are used.

Capacitively coupled feedback

As more and more power supplies now use digital controllers, the use of digital isolators is also becoming more prevalent. The feedback path is no longer purely analogue, but the output voltage is sampled and converted into a digital control signal using general purpose microprocessors or custom DSPs (Digital Signal Processors). The DSP can be either on the primary side for a full digital control topology or on the secondary side sending back data to modulate an analogue primary side controller or two microprocessors can be used to send data back and forth. The advantage of a microprocessor on the primary side is a guaranteed start up but at the cost of needing to generate a clean low voltage supply from the high voltage mains supply. The advantage of a microprocessor on the output side is that the microprocessor power supply is much simpler, and the ability to have multiple outputs or switchable constant voltage or constant current modes. The disadvantage is that start up into a short circuit may be compromised.

Microprocessors are nowadays so cheap that it is often easier to use them on both the primary and secondary sides and use a digital isolator to communicate between them. Capacitively coupled digital isolators off er very high isolation (typically 5kVAC/1 minute) in a very compact package with cleaned-up outputs with well controlled slew rates.

Capacitively coupled digital isolators come in two main fl avours: modulated or edge triggered. A modulated digital isolator consists of a capacitively coupled modulator and demodulator than run at a much higher frequency than the signal bandwidth being transmitted. Data is transmitted by On-Off Keying (OOK) meaning that the digital input is simply used to gate a high frequency oscillator typically running at 10s of Megahertz, so data rates from DC up to 100Mbps are possible.



The disadvantage of using modulated couplers is the very high internal operating frequency which can cause EMI problems if a spread spectrum oscillator is not used or if the PCB layout is not carefully designed with lots of decoupling capacitors and separated ground/power planes.

The relatively slow reaction time of the demodulator creates a propagation delay of 10-100ns, which for fast control loops may be signifi cant delay. The alternative is to use edge triggered communication:



Edge triggered digital isolators have lower propagation delays and higher data throughput than modulated digital isolators, but are more expensive and despite the differential inputs can be more susceptible to interference from stray electric fields.

Primary side regulation

Although digital isolators find many uses in high end, space and defense applications, they are too expensive for many cost sensitive industrial and commercial power supplies. Primary side regulation (PSR) is the most commonly used method as even the cost of the optocoupler can be significant in a design with a BoM budget of only a few dollars. PSR also has the advantage that the auxiliary winding is needed in any case to bootstrap power the controller IC and to reduce the power lost in the start-up resistor chain. A typical IC-based PSR topology is shown below, along with the waveforms.





There are four distinct phases of operation:
Phase 1: The MOSFET is gated on and current through the primary winding increases linearly until it reaches the peak current limit, I_pk, which is detected by measuring the voltage across the sense resistor, R_s.

Phase 2: The MOSFET is turned off and the energy stored in the core is released through the output diode as the magnetic fi eld collapses. The current through the diode decreases from a peak current of I_pk times the primary to secondary turns ratio, Np: Ns linearly down to zero.

Phase 3: The voltage on the auxiliary winding, V_AW, meanwhile decreases from a peak voltage of the auxiliary to secondary turns ratio multiplied by (Vout + diode drop, V_F) to just Na:Ns multiplied by Vout as the diode current decreases to zero. At this point the auxiliary winding voltage is sampled via the resistor divider R1 and R2. The resistor divider ratio is the opposite of the auxiliary turns ratio, so the voltage on V_FB is simply the output voltage. This is used to regulate the PWM controller.

Phase4: The transformer goes into quasi-resonant mode. The auxiliary voltage is monitored for the next valley before restarting the cycle. This allows the main power MOSFET to switch on at the minimum primary voltage to reduce the switching stress.

The big advantage of PSR is the low component count as the necessary PWM control, sample–and-hold and protection circuitry is all integrated inside the control IC. The auxiliary winding does not just eliminate the need for an opto-coupler, it also provides enough bootstrap power to run the IC. A high value resistor chain R_HV1 + R_HV2 from the rectified input voltage is used to start up the IC, but as soon as it is running, the IC switches to the rectified low voltage supply from the auxiliary output via R_supply and D1. This reduces the power consumption considerably and increases the efficiency.

The disadvantages are the need for an auxiliary winding. This does not add much cost, but can make the transformer construction more complex, especially if split primary windings are used. The windings need to be carefully arranged so that the insulation withstand voltage and the clearances are not affected by the extra winding. Also the topology require discontinuous operation to sample the reflected output voltage on the auxiliary winding correctly, and this makes constant current converters more difficult to design to ensure DCM under all operating conditions.

Also a dummy load resistor, R_Lmin, is needed to keep the switching frequency above a minimum limit and to stop the output voltage rising out of specification under no-load conditions (refer to the next chapter for low power consumption techniques)

In general, the advantages outweigh the disadvantages to such an extent that quasi-resonant PSR is the most commonly used AC/DC topology for almost all low power converters.